
Jak przekonwertować liczby binarne na dziesiętne:
- Krok 1: Zapisz wagę przypisaną każdej cyfrze liczby binarnej. Waga ta jest równa 2 potęgom pozycji cyfry w liczbie czytanej od prawej do lewej strony.
- Krok 2: Teraz należy zanotować wagę, dla której wartość binarna jest równa 1.
- Krok 3: Dodaj wszystkie liczby otrzymane w poprzednim kroku
- Krok 4: Liczba z ostatniego kroku będzie dziesiętnym odpowiednikiem liczby binarnej.
Weźmy pod uwagę wartość binarną 1101001.
1.) Krok pierwszy:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Związane z wagą} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Krok drugi: Wagi, dla których cyfry binarne mają wartość 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Krok trzeci: Dodanie wszystkich wag
$$105 = 64 + 32 + 8 + 1$$
4.) Ostatni krok: Binarny odpowiednik w systemie dziesiętnym to:: 105
Jak przekonwertować liczby dziesiętne na binarne:
Po wykonaniu tych czynności można przekonwertować dowolną liczbę dziesiętną na system binarny:
- Krok 1: Podziel liczbę dziesiętną przez 2, zapisz resztę i przypisz jej wartość R1 = reszta, podobnie przypisz wartość Q1 = iloraz otrzymany w tym dzieleniu.
- Krok 2: Teraz podziel Q1 przez 2 i zanotuj resztę. Przypisz wartość reszty do R2, a wartość ilorazu do Q1.
- Krok 3: Kontynuuj tę sekwencję, aż w pewnym momencie dzielenia otrzymasz wartość ilorazu (Qn) równą 0.
- Krok 4: Liczbę binarną można zapisać jako: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINARY
Jak zamieniać cyfry po przecinku między systemem dwójkowym a dziesiętnym?
Do tej pory dowiedzieliśmy się, jak zamieniać liczby całkowite na binarne i dziesiętne. A co z liczbami z miejscami dziesiętnymi? Procedura jest podobna do powyższych kroków. Najpierw dzielimy liczbę na część przed i po miejscu dziesiętnym. Weźmy pod uwagę liczbę dziesiętną 1932,1875:
Składa się ona z części całkowitej 1932 oraz ułamka 0,1875. Dla części całkowitej 1932 wykonaj czynności opisane powyżej. Otrzymany w ten sposób odpowiednik binarny to: 11110001100.
Część ułamkową 0,1875 można przekonwertować według następującego schematu. Rekursywnie pomnóż część ułamkową przez dwa. Jeśli wynik jest większy od 1, zapisz 1, a następnie odejmij 1 od otrzymanej liczby. Jeśli wynik jest mniejszy niż jeden, zapisz 0. Następnie kontynuuj mnożenie przez dwa. W przeciwnym razie zapisz 0.
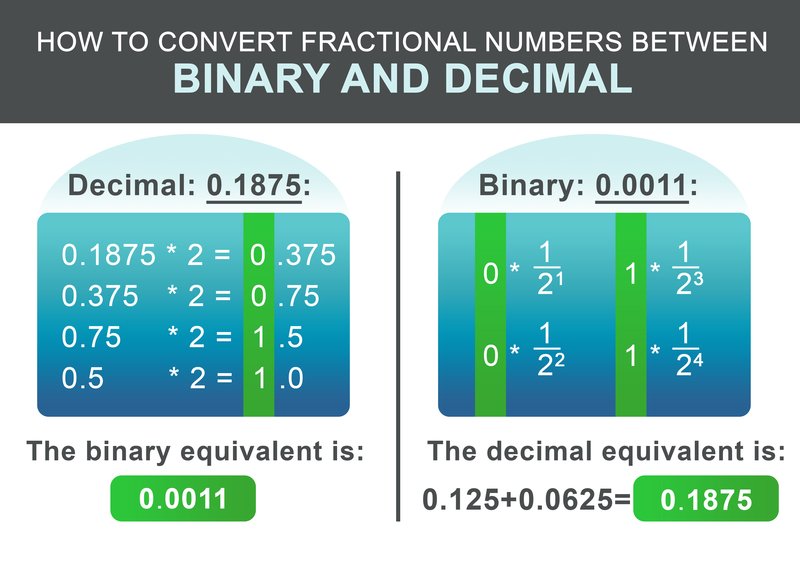
Dla naszego przykładu 0,1875 wynikowa liczba binarna to: 0,0011 W ostatnim kroku dodajemy części całkowite i ułamkowe:
$$11110001100.0011$$
W przypadku konwersji binarnej sposób postępowania jest jeszcze prostszy. Dodaj do wyniku $1/2^i$ dla każdej cyfry po kropce, przy czym i jest pozycją cyfry po kropce od lewej do prawej, zaczynając od 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
System liczb binarnych i jego zastosowania
System liczbowy to zbiór różnych kombinacji symboli, przy czym każdy symbol ma określoną wagę. Główną cechą systemu liczbowego jest radix lub podstawa, która określa całkowitą liczbę symboli używanych w danym systemie liczbowym. Na przykład radix systemu liczb binarnych to 2, a radix systemu liczb dziesiętnych to 10.
Przestrzeń cyfr systemu binarnego
W systemie binarnym mamy dwie różne cyfry: 0 i 1. W komputerach mamy urządzenia takie jak przerzutniki, które mogą przechowywać dowolny z tych dwóch poziomów zgodnie z sygnałem sterującym. Wyższemu poziomowi przypisana jest wartość 1, a niższemu poziomowi - wartość 0, tworząc w ten sposób system binarny.
Znaczenie systemu binarnego w informatyce:
Komputer korzysta z miliardów i miliardów tranzystorów, które działają w sposób cyfrowy. Termin "cyfrowy" odnosi się do dyskretnych poziomów logicznych. Poziomy logiczne to różne poziomy potencjału, takie jak 5 V, 0 V, 10 V i wiele innych.
Każdy komputer działa w oparciu o logikę binarną, więc jeśli chcemy przedstawić komputer, musimy zapisywać liczby z radixem równym 2. Dwa symbole w tym systemie liczbowym są analogiczne do dwóch dyskretnych poziomów logicznych. Dla ułatwienia traktujemy te dwa symbole jako 0 i 1, ale dla komputera 0 i 1 to różne poziomy napięcia. Ogólnie rzecz biorąc, 0 oznacza niższy poziom napięcia, a 1 - wyższy poziom napięcia.
Wszystko, co widzimy na ekranie komputera lub wprowadzamy za pomocą myszy lub klawiatury, to same 0 i 1, a jedyną różnicą jest ich sekwencyjne ułożenie. Jeśli więc chcemy wykonać naszą pracę na komputerze, musimy wiedzieć, jak działa system binarny i jaki jest związek systemu binarnego z dziesiętnym, aby móc przekształcić wartości z dziedziny binarnej na naszą znaną dziedzinę.
