
Cách chuyển đổi số nhị phân sang thập phân:
- Bước 1: Ghi lại trọng số liên kết dưới mỗi chữ số trong số nhị phân. Trọng số là 2 mũ vị trí của chữ số trong số khi đọc từ phải sang trái.
- Bước 2: Bây giờ ghi chú trọng lượng mà giá trị nhị phân bằng 1.
- Bước 3: Cộng tất cả các số thu được ở bước trước
- Bước 4: Số từ bước trước sẽ là phần thập phân tương ứng của số nhị phân.
Hãy xem xét giá trị nhị phân 1101001.
Bước 1:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY: Nhị phân} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Trọng lượng liên quan} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Bước thứ hai: Trọng số mà các số nhị phân là 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Bước thứ ba: Thêm tất cả các trọng lượng
$$105 = 64 + 32 + 8 + 1$$
4.) Bước cuối cùng: Giá trị thập phân tương đương của số nhị phân là:: 105
Cách chuyển đổi Số thập phân thành Nhị phân:
The meaning of the above statement in Vietnamese is not clear. Could you please provide more context or specific instructions?
- Bước 1: Chia số thập phân cho 2 và ghi lại phần dư, gán giá trị R1 = phần dư, tương tự gán giá trị Q1 = phần thương thu được trong phép chia này.
- Bước 2: Bây giờ chia Q1 cho 2 và ghi lại phần dư. Gán giá trị của phần dư vào R2 và giá trị của thương vào Q1.
- Bước 3: Tiếp tục chuỗi cho đến khi tại một điểm nào đó trong phép chia bạn nhận được giá trị thương (Qn) bằng 0.
- Bước 4: Bạn có thể viết số nhị phân như sau: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) Hệ thập phân = (10110011) BINARY: Nhị phân
Làm thế nào để chuyển đổi các chữ số sau dấu thập phân giữa hệ thống số nhị phân và thập phân?
Cho đến nay, chúng ta đã học cách chuyển đổi số nguyên giữa hệ nhị phân và thập phân. Vậy còn số có phần thập phân thì sao? Thủ tục tương tự như các bước trên. Đầu tiên, chia số thành phần trước và sau dấu thập phân. Hãy xem xét số thập phân 1932.1875:
Nó bao gồm một phần nguyên là 1932 và phần phân số 0.1875. Đối với phần nguyên 1932, sử dụng các bước từ trên. Kết quả tương đương nhị phân là: 11110001100.
Phần phân số 0,1875 có thể được chuyển đổi theo hướng dẫn sau. Đệ quy nhân phần phân số với hai. Nếu kết quả vượt quá 1, ghi lại số 1 và sau đó trừ 1 từ số kết quả. Nếu kết quả nhỏ hơn một, ghi lại số 0. Tiếp theo, tiếp tục nhân với hai. Nếu không, ghi lại số 0.
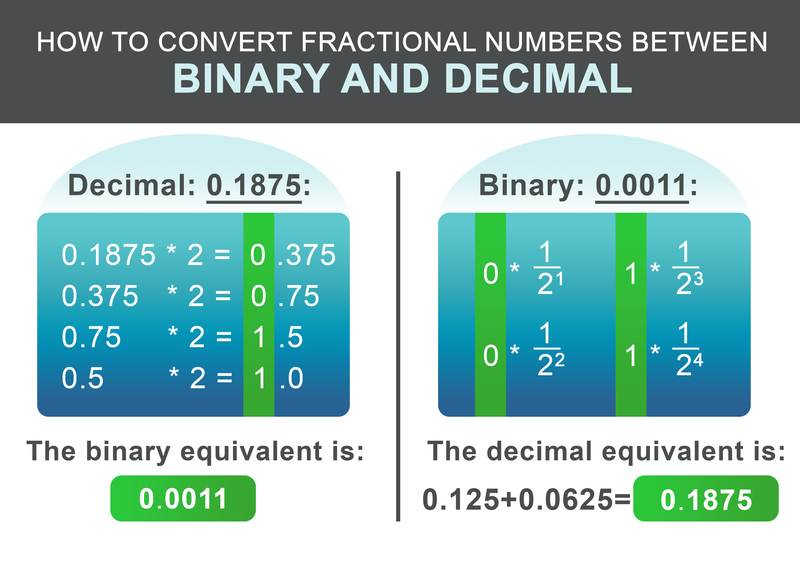
Với ví dụ của chúng ta, số nhị phân kết quả là: 0.0011 Trong bước cuối cùng, thêm phần nguyên và phân số vào nhau.
$$11110001100.0011$$
Để chuyển đổi số nhị phân về dạng phân số, quy trình là ngay cả đơn giản hơn. Thêm $1/2^i$ cho mỗi chữ số sau dấu chấm vào kết quả, trong đó i là vị trí của chữ số tính từ trái sang phải, bắt đầu từ 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Hệ thống số nhị phân và ứng dụng của nó
Hệ thống số là một tập hợp các kết hợp khác nhau của các ký hiệu, với mỗi ký hiệu có một trọng số cụ thể. Đặc điểm chính của một hệ thống số là cơ số hoặc cơ số xác định tổng số ký hiệu được sử dụng trong một hệ thống số cụ thể. Ví dụ, cơ số của hệ thống số nhị phân là 2 và cơ số của hệ thống số thập phân là 10.
Không gian chữ số của hệ thống nhị phân
Trong hệ nhị phân, chúng ta có hai số khác biệt: 0 và 1. Trong máy tính, chúng ta có các thiết bị như flip-flop có thể lưu trữ một trong hai mức theo tín hiệu điều khiển. Mức cao được gán giá trị 1 và mức thấp được gán giá trị 0, do đó tạo thành một hệ nhị phân.
Tầm quan trọng của hệ thống nhị phân trong tính toán:
Một máy tính sử dụng hàng tỷ transistor hoạt động kỹ thuật số. Thuật ngữ kỹ thuật số liên quan đến các mức logic rời rạc. Các mức logic là các mức tiềm năng khác nhau như 5V, 0V, 10V và nhiều mức khác.
Máy tính hoạt động dựa trên một logic nhị phân, vì vậy nếu chúng ta muốn biểu diễn máy tính, chúng ta phải viết các số với cơ số bằng 2. Hai ký tự trong hệ thống số này tương đương với hai mức logic rời rạc. Để tiện cho việc sử dụng, chúng ta coi hai ký tự này là 0 và 1, nhưng đối với máy tính, 0 và 1 là mức điện áp khác nhau. Thông thường, 0 được coi là mức điện áp thấp hơn và 1 được coi là mức điện áp cao hơn.
Tất cả những gì chúng ta thấy trên màn hình máy tính hoặc cung cấp đầu vào thông qua chuột hoặc bàn phím đều là 0 và 1, sự khác biệt duy nhất là sự sắp xếp tuần tự của chúng. Vì vậy, nếu chúng ta muốn hoàn thành công việc từ máy tính, chúng ta phải biết cách làm việc của hệ nhị phân và mối quan hệ của nó với hệ thập phân để chuyển đổi giá trị từ miền nhị phân sang miền đã biết của chúng ta.
