
Kuinka muuntaa binääriluvut desimaaliluvuksi:
- Vaihe 1: Kirjoita binääriluvun jokaisen numeron alapuolella oleva paino. Paino on 2 luvun numeron sijainnin potenssilla numerossa oikealta vasemmalle.
- Vaihe 2: Merkitään nyt paino, jonka binääriarvo on 1.
- Vaihe 3: Lasketaan yhteen kaikki edellisessä vaiheessa saadut luvut.
- Vaihe 4: Viimeisen vaiheen luku on binääriluvun desimaalinen vastine.
Tarkastellaan binääriarvoa 1101001.
1.) Ensimmäinen vaihe:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Painoon liittyvä} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Toinen vaihe: Painot, joiden binääriluvut ovat 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Kolmas vaihe: Kaikkien painojen lisääminen
$$105 = 64 + 32 + 8 + 1$$
4.) Viimeinen vaihe: Binaryn desimaaliluku on:: 105
Kuinka muuntaa desimaaliluvut binääriluvuiksi:
Näiden vaiheiden avulla voit muuntaa minkä tahansa desimaaliluvun binäärijärjestelmään:
- Vaihe 1: Jaa desimaaliluku kahdella, kirjoita jäännös ja anna arvo R1 = jäännös, ja anna vastaavasti arvo Q1 = jakolasku.
- Vaihe 2: Jaa nyt Q1 luvulla 2 ja merkitse jäännös. Määritä jäännöksen arvo R2:lle ja osamäärän arvo Q1:lle.
- Vaihe 3: Jatka sarjaa, kunnes jossakin vaiheessa jakoa saat osamäärän (Qn) arvoksi 0.
- Vaihe 4: Voit kirjoittaa binääriluvun seuraavasti: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINARY
Miten desimaalipisteen jälkeiset numerot muunnetaan binääri- ja desimaalilukujärjestelmän välillä?
Tähän mennessä olemme oppineet muuntamaan kokonaislukuja binääri- ja desimaalilukujen välillä. Entä luvut, joissa on desimaalilukuja? Menettely on samanlainen kuin edellä. Jaa luku ensin ennen ja jälkeen desimaalipisteen. Tarkastellaan desimaalilukua 1932,1875:
Se koostuu kokonaisluvusta 1932 ja murtoluvusta 0,1875. Käytä kokonaislukuosan 1932 osalta edellä esitettyjä vaiheita. Tuloksena on seuraava binäärinen vastine: 11110001100.
Murtoluku 0,1875 voidaan muuntaa seuraavan kaavion mukaisesti. Kerro murtolukuosa kahdella. Jos tulos on suurempi kuin 1, merkitään 1 ja vähennetään sitten 1 saadusta luvusta. Jos tulos on pienempi kuin 1, merkitään 0. Jatketaan seuraavaksi kertomista kahdella. Muussa tapauksessa merkitään 0.
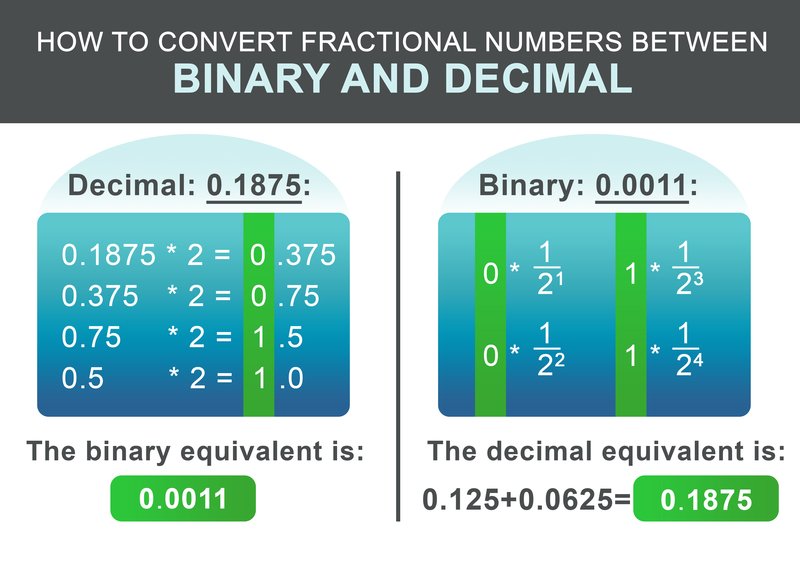
Esimerkissämme 0,1875 tuloksena saadaan binääriluku: 0,0011 Viimeisessä vaiheessa lisätään kokonaisluku ja murtoluku:
$$11110001100.0011$$
Binäärisen fraktion muuntaminen takaisin on vielä yksinkertaisempaa. Lisää tulokseen $1/2^i$ jokaista pisteen jälkeistä numeroa kohden, jolloin i on sen jälkeisen numeron sijainti vasemmalta oikealle alkaen 1:stä.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Binäärilukujärjestelmä ja sen sovellukset
Lukujärjestelmä on joukko erilaisia symboliyhdistelmiä, joissa kullakin symbolilla on tietty painoarvo. Lukujärjestelmän tärkeimmät ominaisuudet ovat radiksi eli perusluku, joka määrittelee tietyssä lukujärjestelmässä käytettyjen symbolien kokonaismäärän. Esimerkiksi binäärilukujärjestelmän radix on 2 ja desimaalilukujärjestelmän radix on 10. Tämän järjestelmän radix on 2.
Binäärijärjestelmän numeroavaruus
Binäärijärjestelmässä on kaksi erillistä numeroa: Tietokoneissa on flip-floppien kaltaisia laitteita, jotka voivat tallentaa minkä tahansa näistä kahdesta tasosta ohjaussignaalin mukaan. Korkeammalle tasolle annetaan arvo 1 ja alemmalle tasolle arvo 0, jolloin muodostuu binäärijärjestelmä.
Binäärijärjestelmän merkitys tietojenkäsittelyssä:
Tietokone käyttää miljardeja ja taas miljardeja transistoreja, jotka toimivat digitaalisesti. Termi digitaalinen liittyy erillisiin loogisiin tasoihin. Logiikkatasot ovat erilaisia potentiaalitasoja, kuten 5V, 0V, 10V ja monia muita.
Kaikki tietokoneet toimivat binäärilogiikan avulla, joten jos haluamme esittää tietokoneen, meidän on kirjoitettava numerot radixilla 2. Tämän lukujärjestelmän kaksi symbolia vastaavat kahta diskreettia logiikan tasoa. Helppouden vuoksi pidämme näitä kahta symbolia 0:na ja 1:nä, mutta tietokoneessa 0 ja 1 ovat eri jännitetasoja. Yleensä 0 on pienempi jännitetaso ja 1 suurempi jännitetaso.
Kaikki, mitä näemme tietokoneen näytöllä tai annamme syötteen hiiren tai näppäimistön kautta, ovat kaikki 0- ja 1-nollia, ainoa ero on niiden järjestysjärjestys. Jos siis haluamme saada työmme tehtyä tietokoneella, meidän on tiedettävä, miten binääri toimii ja mikä on binäärin suhde desimaalilukuihin, jotta voimme muuntaa arvot binäärialueelta meille tunnetuksi alueeksi.
