
Как да конвертирате двоични числа в десетични:
- Стъпка 1: Запишете теглото, свързано под всяка цифра на двоичното число. Теглото е 2 по степента на позицията на цифрата в числото, като се чете отдясно наляво.
- Стъпка 2: Сега отбележете теглото, за което двоичната стойност е равна на 1.
- Стъпка 3: Съберете всички числа, получени в предишната стъпка
- Стъпка 4: Числото от последната стъпка ще бъде десетичният еквивалент на двоичното число.
Нека разгледаме двоична стойност 1101001.
1.) Първа стъпка:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Свързано с теглото} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Втора стъпка: Тегла, за които двоичните цифри са 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Трета стъпка: Добавяне на всички тегла
$$105 = 64 + 32 + 8 + 1$$
4.) Последна стъпка: Десетичният еквивалент на двоичната система е:: 105
Как да конвертирате десетични числа в двоични:
Следвайки тези стъпки, можете да преобразувате всяко десетично число в двоична система:
- Стъпка 1: Разделете десетичното число на 2, запишете остатъка и присвоете стойност R1 = остатък, като по същия начин присвоите стойността Q1 = коефициент, получен при това деление.
- Стъпка 2: Сега разделете Q1 на 2 и запишете остатъка. Припишете стойността на остатъка на R2, а стойността на коефициента - на Q1.
- Стъпка 3: Продължете последователността, докато в даден момент от делението получите стойност на коефициента (Qn), равна на 0.
- Стъпка 4: Можете да запишете двоичното число като: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) ДЕЦИМАЛЕН = (10110011) BINARY
Как се преобразуват цифрите след десетичната запетая между двоичната и десетичната бройна система?
Досега научихме как да преобразуваме цели числа в двоична и десетична бройна система. Какво ще кажете за числата с десетичен знак? Процедурата е подобна на горните стъпки. Първо, разделете числото на частта му преди и след десетичния знак. Нека разгледаме десетичното число 1932,1875:
Състои се от цяло число 1932 и дробта 0,1875. За целочислената част 1932 използвайте стъпките от по-горе. Полученият двоичен еквивалент е: 11110001100.
Дробната част 0,1875 може да се преобразува по следната схема. Рекурсивно умножете дробната част по две. Ако резултатът е по-голям от 1, запишете 1 и след това извадете 1 от полученото число. Ако резултатът е по-малък от единица, запишете 0. След това продължете да умножавате по две. В противен случай запишете 0.
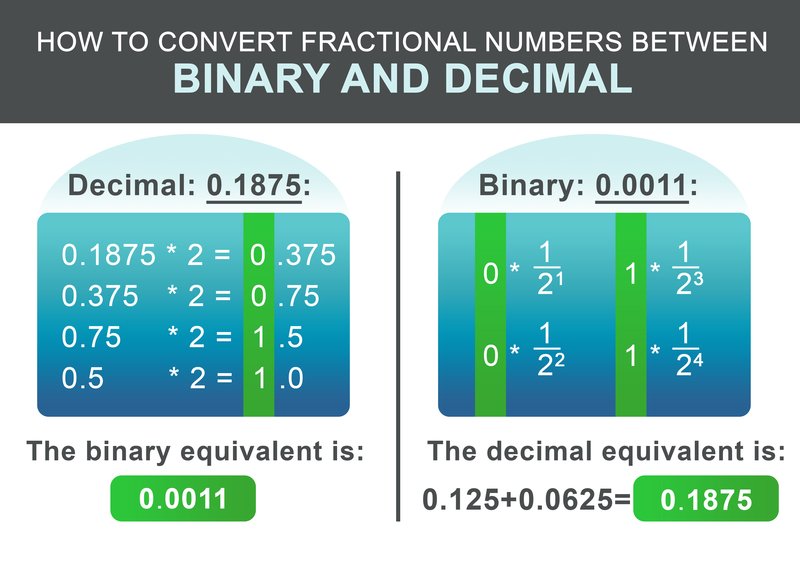
За нашия пример 0.1875 полученото двоично число е: 0.0011 В последната стъпка добавете целочислените и дробните части:
$$11110001100.0011$$
За преобразуване на бинарната фракция обратно работният процес е още по-прост. Добавете $1/2^i$ за всяка цифра след точката към резултата, като i е позицията на цифрата след нея от ляво на дясно, започвайки от 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Двоична бройна система и нейните приложения
Цифровата система е набор от различни комбинации от символи, като всеки символ има определено тегло. Основните характеристики на една бройна система са радиксът или основата, която определя общия брой символи, използвани в конкретната бройна система. Например радиксът на двоичната бройна система е 2, а радиксът на десетичната бройна система е 10.
Цифровото пространство на двоичната система
В двоичната система имаме две различни цифри: В компютрите имаме устройства като флип-флопове, които могат да съхраняват всяко от двете нива в зависимост от управляващ сигнал. На по-високото ниво се присвоява стойност 1, а на по-ниското ниво се присвоява стойност 0, като по този начин се образува двоична система.
Значение на двоичната система в изчислителната техника:
Компютърът се състои от милиарди и милиарди транзистори, които работят цифрово. Терминът "цифров" се отнася до дискретните логически нива. Логическите нива са различните потенциални нива като 5 V, 0 V, 10 V и много други.
Всеки компютър работи с двоична логика, така че ако искаме да представим компютъра, трябва да запишем числата с радикс, равен на 2. Двата символа в тази бройна система са аналогични на двете дискретни логически нива. За наше улеснение разглеждаме тези два символа като 0 и 1, но за компютъра 0 и 1 са различни нива на напрежение. Обикновено 0 се счита за по-ниско ниво на напрежение, а 1 - за по-високо ниво на напрежение.
Всичко, което виждаме на екрана на компютъра или въвеждаме чрез мишката или клавиатурата, са все 0 и 1, като единствената разлика е в последователното им подреждане. Така че, ако искаме да свършим работата си от компютъра, трябва да знаем как работи двоичната система и каква е връзката на двоичната система с десетичната, за да преобразуваме стойностите от двоичната област в познатата ни област.
