
如何将二进制数转换为十进制数。
- 第1步:写下二进制数字的每个数字下面的相关重量。权重是数字位置的2次方,从右到左读。
- 第二步:现在注意二进制值等于1的权重。
- 第3步:将上一步中得到的所有数字相加。
- 第四步:上一步的数字将是二进制数字的十进制等值。
让我们考虑一个二进制值1101001。
1.)第一个步骤。
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{相关重量} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.)第二步。 二进制数字为1的权重。
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.)第三步。将所有的权重相加
$$105 = 64 + 32 + 8 + 1$$
4.)最后一步。二进制的十进制等价物是。: 105
如何将十进制数字转换为二进制。
按照这些步骤,你可以将任何十进制数字转换成二进制系统。
- 第一步:用小数点后的数字除以2,写下余数并赋值R1=余数,同样赋值Q1=此次除法得到的商。
- 第二步:现在用Q1除以2,记下余数。将余数的值分配给R2,将商的值分配给Q1。
- 第3步:继续这个序列,直到在除法的某个时刻,你得到的商(Qn)的值等于0。
- 第4步:你可以把二进制数写成。 $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) 小数点 = (10110011) BINARY
如何在二进制和十进制数字系统之间转换小数点之后的数字?
到目前为止,我们已经学会了如何在二进制和十进制之间转换整数。那么,带有小数位的数字呢?这个过程与上面的步骤类似。首先,将数字分成小数点前和小数点后的部分。让我们考虑一下十进制数字1932.1875。
它由一个整数部分1932和分数0.1875组成。对于1932的整数部分,使用上面的步骤。由此产生的二进制等价物是。11110001100.
小数部分0.1875可以按照以下模式进行转换。递归地将派生部分乘以2。 如果结果超过1,写下1,然后从所得的数字中减去1。如果结果小于1,就写下0,然后继续乘以2。 否则就写下0。
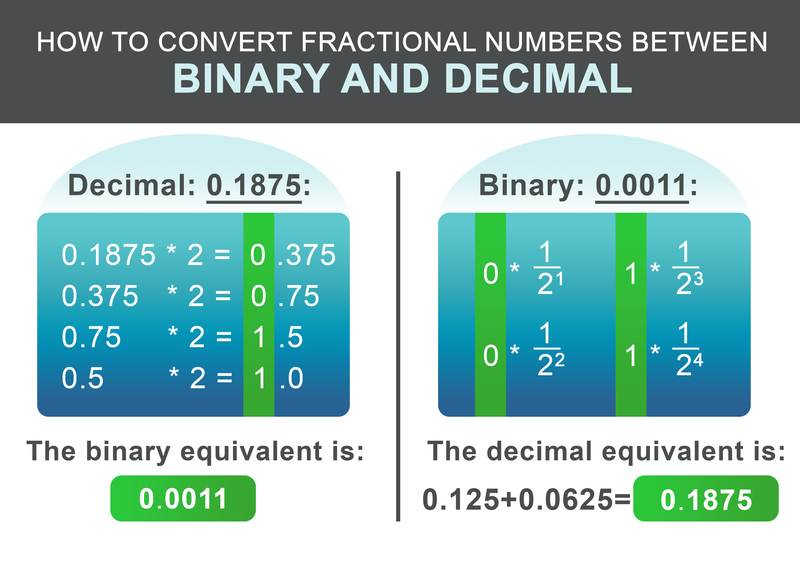
对于我们的例子0.1875,得到的二进制数是:0.0011 在最后一步,将整数和小数部分相加。
$$11110001100.0011$$
对于将二进制派别转换回来,工作流程更加简单。 在结果中为点后面的每个数字加上1/2^i$,其中i是后面数字的位置,从左到右,从1开始。
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
二进制数系统及其应用
一个数字系统是一组不同的符号组合,每个符号都有一个特定的权重。一个数字系统的主要特征是定义了特定数字系统中使用的符号总数的拉德数或基数。例如,二进制数系统的基数是2,而十进制数系统的基数是10。
二进制系统的数字空间
在二进制系统中,我们有两个不同的数字。在计算机中,我们有像触发器这样的设备,可以根据控制信号来存储这两个级别中的任何一个。较高的级别被分配为1,较低的级别被分配为0,因此形成一个二进制系统。
二进制系统在计算中的重要性。
一台计算机使用了数十亿的晶体管,以数字方式运行。数字化一词与离散的逻辑电平有关。逻辑电平是不同的电位水平,如5V、0V、10V和许多其他电位水平。
任何计算机都是使用二进制逻辑运行的,所以如果我们想表示计算机,我们必须写出弧度等于2的数字。这个数字系统中的两个符号类似于两个离散的逻辑电平。为了方便起见,我们把这两个符号看作是0和1,但对于计算机来说,0和1是不同的电压水平。一般来说,0被认为是较低的电压水平,1被认为是较高的电压水平。
我们在计算机屏幕上看到的或通过鼠标或键盘提供的输入都是0和1,唯一的区别是它们的顺序排列。因此,如果我们想通过计算机完成我们的工作,我们必须知道二进制是如何工作的,以及二进制与小数的关系是什么,以便将数值从二进制领域转换到我们的已知领域。
