
Jak převést binární čísla na desítková:
- Krok 1: Zapište váhu přiřazenou pod každou číslici binárního čísla. Váha je 2 na mocninu pozice číslice v čísle čtené zprava doleva.
- Krok 2: Nyní zaznamenejte váhu, pro kterou je binární hodnota rovna 1.
- Krok 3: Sečtěte všechna čísla získaná v předchozím kroku.
- Krok 4: Číslo z posledního kroku bude desítkovým ekvivalentem binárního čísla.
Uvažujme binární hodnotu 1101001.
1.) První krok:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÁRNÍ} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Hmotnost související} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Druhý krok: Váhy, pro které jsou binární číslice 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Třetí krok: Sčítání všech vah
$$105 = 64 + 32 + 8 + 1$$
4.) Poslední krok: Decimální ekvivalent binárního tvaru je:: 105
Jak převést desítková čísla na dvojková:
Podle těchto kroků můžete převést libovolné desítkové číslo do dvojkové soustavy:
- Krok 1: Vydělte desetinné číslo dvěma, zapište zbytek a přiřaďte hodnotu R1 = zbytek, podobně přiřaďte hodnotu Q1 = kvocient získaný tímto dělením.
- Krok 2: Nyní vydělte Q1 číslem 2 a zapište si zbytek. Hodnotu zbytku přiřaďte R2 a hodnotu kvocientu Q1.
- Krok 3: Pokračujte v posloupnosti, dokud v některém bodě dělení nedostanete hodnotu kvocientu (Qn) rovnou 0.
- Krok 4: Binární číslo můžete zapsat jako: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINÁRNÍ
Jak se převádějí číslice za desetinnou čárkou mezi dvojkovou a desítkovou číselnou soustavou?
Dosud jsme se učili převádět celá čísla mezi dvojkovou a desítkovou soustavou. Jak je to s čísly s desetinnými místy? Postup je podobný výše uvedeným krokům. Nejprve rozdělte číslo na část před a za desetinným místem. Uvažujme desetinné číslo 1932,1875:
Skládá se z celočíselné části 1932 a zlomku 0,1875. Pro celočíselnou část 1932 použijte postup uvedený výše. Výsledný binární ekvivalent je: 11110001100.
Zlomek 0,1875 lze převést podle následujícího schématu. Rekurzivně vynásobte zlomkovou část dvěma. Pokud je výsledek větší než 1, zapište 1 a od výsledného čísla odečtěte 1. Pokud je výsledek menší než 1, zapište 0. Dále pokračujte v násobení dvěma. V opačném případě zapište 0.
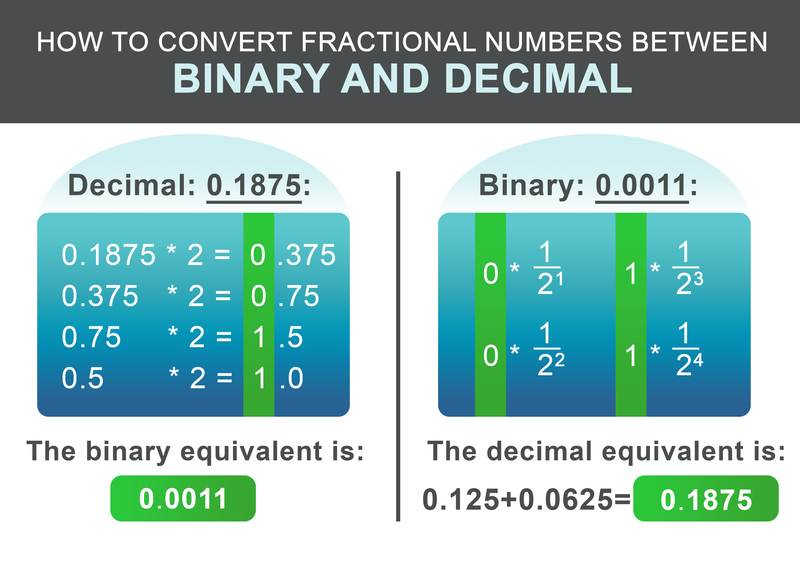
Pro náš příklad 0,1875 je výsledné binární číslo: 0,0011 V posledním kroku sečteme celočíselné a zlomkové části:
$$11110001100.0011$$
Při zpětném převodu binární frakce je pracovní postup ještě jednodušší. K výsledku přičtěte $1/2^i$ za každou číslici za tečkou, přičemž i je pozice číslice za zleva doprava, počínaje jedničkou.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Binární číselná soustava a její aplikace
Číselná soustava je soubor různých kombinací symbolů, přičemž každý symbol má určitou váhu. Hlavní charakteristikou číselné soustavy je radix nebo základ, který určuje celkový počet symbolů použitých v dané číselné soustavě. Například radix binární číselné soustavy je 2 a radix desítkové číselné soustavy je 10.
Digitální prostor dvojkové soustavy
Ve dvojkové soustavě máme dvě různé číslice: V počítačích máme zařízení, jako jsou klopné obvody, které mohou ukládat libovolnou z těchto dvou úrovní podle řídicího signálu. Vyšší úrovni je přiřazena hodnota 1 a nižší úrovni je přiřazena hodnota 0, čímž vzniká binární soustava.
Význam dvojkové soustavy ve výpočetní technice:
Počítač využívá miliardy a miliardy tranzistorů, které pracují digitálně. Pojem digitální se týká diskrétních logických úrovní. Logické úrovně jsou různé potenciální úrovně jako 5 V, 0 V, 10 V a mnoho dalších.
Každý počítač pracuje s binární logikou, takže pokud chceme počítač reprezentovat, musíme čísla zapisovat s radixem rovným 2. Dva symboly v této číselné soustavě jsou analogické dvěma diskrétním logickým úrovním. Pro naše usnadnění považujeme tyto dva symboly za 0 a 1, ale pro počítač jsou 0 a 1 různé úrovně napětí. Obecně se 0 považuje za nižší napěťovou úroveň a 1 za vyšší napěťovou úroveň.
Vše, co vidíme na obrazovce počítače nebo zadáváme prostřednictvím myši či klávesnice, jsou samé nuly a jedničky, liší se pouze jejich pořadovým uspořádáním. Chceme-li tedy z počítače dostat svou práci, musíme vědět, jak funguje dvojková soustava a jaký je vztah dvojkové soustavy s desetinnými čísly, abychom mohli převádět hodnoty z dvojkové oblasti do nám známé oblasti.
